Asignatura: Diseño y Procesamiento mecánico

Curso: 4° Mecánica

Profesor: Ariel Lauritto

email: rariel_lauritto@yahoo.com.ar

El proceso de corte ortogonal

Actividades:

1) Definición y parámetros del corte octogonal.

2)  ¿Qué velocidades intervienen en el corte octogonal?

3) ¿Qué fuerzas intervienen?

4) ¿Qué es la viruta? Tipos: describir

 Definición y parámetros característicos del corte ortogonal

Como ya se ha comentado en apartados anteriores, los procesos de mecanizado son complejos de analizar debido a la multitud de factores que entran en juego (geometría y tipo de material de la pieza a mecanizar, geometría y tipo de material de la herramienta de corte, profundidad y velocidad de corte, temperatura, etc.).

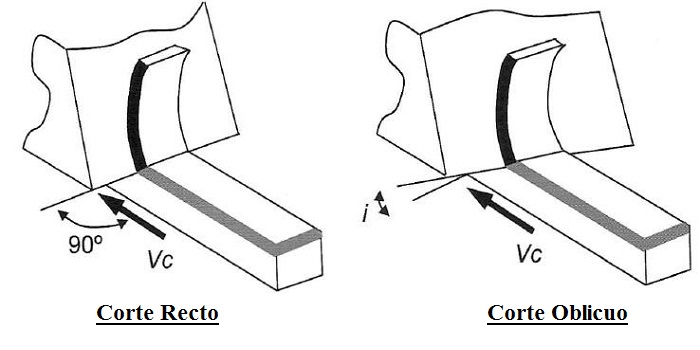
Sin embargo, para simplificar el análisis de los procesos de mecanizado, es muy común en los modelos de estudios emplear el llamado Modelo de Corte Ortogonal, con objeto de poder interpretar y estudiar de una manera más simple, aunque no por ello menos precisa, aquellos factores y parámetros que intervienen en cualquier proceso de mecanizado.

El corte ortogonal, o corte recto, es un modelo simplificado de analizar el proceso de mecanizado por arranque de viruta que permite calcular los parámetros característicos del corte sin alejarse mucho de la realidad.

En el corte ortogonal, el filo de la herramienta de corte es perpendicular a la dirección de desplazamiento entre herramienta y pieza durante el proceso de corte, mientras que en el corte oblicuo existe un cierto ángulo (i) de inclinación.

Por tanto, en el caso del corte ortogonal las fuerzas actuantes durante el corte se pueden descomponer según dos componentes, en lugar de tres como ocurre con el modelo de corte oblicuo. Esto va a suponer que el uso del modelo de corte ortogonal simplifique mucho el estudio de los procesos de mecanizado.

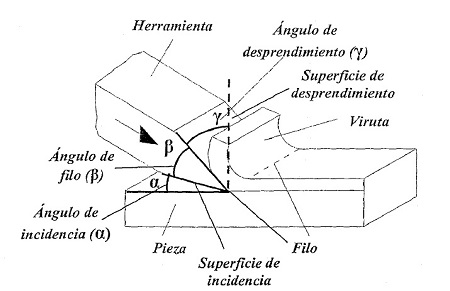
Pero para comprender mejor los parámetros geométricos que definen a un corte ortogonal, es preciso conocer previamente los elementos característicos de una herramienta de corte, como son:

• El filo o arista cortante, que como su nombre indica es la arista o filo de la herramienta que corta el material.

• La superficie de desprendimiento, que es la cara de la herramienta sobre la que desliza el material desprendido.

• La superficie de incidencia, que es la cara de la herramienta que queda frente a la superficie ya mecanizada de la pieza.

En la figura adjunta que se incluye, se representan dichos parámetros geométricos para tener así una mejor comprensión de los mismos.

A continuación, y una vez vistos los parámetros geométricos de la herramienta de corte ya, se pueden definir los ángulos y demás parámetros geométricos que caracterizan al modelo de corte ortogonal:

• Ángulo de desprendimiento (γ):

Es el ángulo formado por la superficie de desprendimiento de la herramienta y la dirección perpendicular a la superficie mecanizada de la pieza.

Este ángulo puede tener un sentido positivo (en sentido horario), o bien sentido negativo, si es en el sentido contrario (sentido antihorario). Así, en función del valor del ángulo de desprendimiento, si éste es mayor que cero las herramientas de corte se clasifican con geometría positiva, y si es menor que cero, las herramientas se clasifican en herramientas con geometría negativa.

Si en un proceso de corte el ángulo de desprendimiento es grande, entonces significaría que la herramienta de corte penetra y corta bien a la pieza, dando lugar a un mejor acabado superficial, pero a costa de ir debilitando mucho el filo de corte.

Por el contrario, si durante el corte el ángulo de desprendimiento es pequeño, entonces se favorecería la resistencia de la herramienta, pero la energía consumida y el calentamiento de la propia herramienta aumentarán.

Para obtener el ángulo de desprendimiento correcto habrá que tener en cuenta la resistencia del material de la herramienta, el tipo de material a mecanizar y el avance. En cualquier caso, el ángulo de desprendimiento adecuado será el mayor que pueda soportar la herramienta sin romperse.

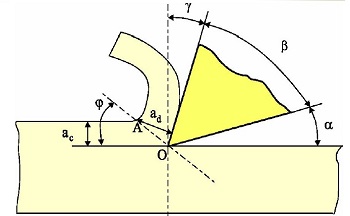
• Ángulo de incidencia (α):

Es el ángulo formado por la superficie de incidencia de la herramienta de corte y la superficie de la pieza ya mecanizada, como se muestra en la figura adjunta.

Si el valor del ángulo de incidencia es muy pequeño, aumentará el contacto entre la herramienta y la pieza, produciéndose un roce excesivo y como consecuencia, un aumento de la temperatura que producirá un desgaste más rápido de la herramienta, y por tanto, disminuirá su vida útil.

Por el contrario, si el valor del ángulo de incidencia es demasiado grande, se debilitaría el filo de la herramienta que afectaría negativamente a su durabilidad. Para conseguir un ángulo de incidencia correcto, habrá que tener en cuenta el material de la pieza y la herramienta.

• Ángulo de filo o ángulo de herramienta (β):

Es el ángulo formado por las superficies de incidencia y desprendimiento de la herramienta de corte.

• Ángulo de deslizamiento o cizalladura (φ):

Es el ángulo formado por la superficie de la pieza y el plano de deslizamiento, que es un plano teórico en el que se produce la deformación del material de la pieza. El ángulo de cizalladura es el ángulo según el cual se corta el material para formar la viruta.

Este ángulo determina la posición del plano de cizallado con respecto el plano que contiene al filo y a la velocidad de corte. Su importancia radica en que por debajo de este plano la pieza de trabajo permanece sin deformaciones, y por encima de él la viruta sale recién formada fluyendo sobre la superficie de desprendimiento.

• Espesor de viruta no deformada (a_c):

Es el espesor del material que va a ser eliminado de la pieza antes de sufrir deformación alguna. O dicho de otra manera, este parámetro también representa a la profundidad de corte.

• Espesor de viruta deformada (a_d):

Es el espesor del material eliminado después de haber sufrido la deformación.

• Factor de recalcado (z):

Es el cociente entre los espesores de viruta deformada y sin deformar. Es siempre mayor o igual que la unidad.

z = a_d / a_c ≥ 1

Definido este factor, el ángulo de cizalladura (φ) también se puede expresar en función del factor de recalcado (z) y del ángulo de desprendimiento (γ), mediante la siguiente expresión:

	cos γ
tan φ =
	z - sen γ

 

 Velocidades que intervienen en el corte ortogonal

En el corte ortogonal intervienen tres velocidades características del proceso de mecanizado: la velocidad de corte (V_c), la velocidad de deformación o velocidad de cizallamiento (V_s) y la velocidad de salida de la viruta (V_v)

•  Velocidad de corte (V_c) : Ya vista en apartados anteriores, es la velocidad lineal relativa de la herramienta respecto de la pieza en la dirección y sentido del movimiento de corte. En los procesos de torneado o fresado esta velocidad se define como:

	π · d · n
Vc =
	1000

donde,

V_c    es la velocidad de corte, expresada en metros por minuto (m/min)

d    es el diámetro de la pieza, en torneado, o el diámetro de la herramienta, si se trata de fresado, expresado en mm.

n    es la velocidad de giro de la pieza, en torneado, o de la herramienta, en fresado, en revoluciones por minuto (r.p.m.)

•  Velocidad de deformación o cizallamiento (V_s) : Es la velocidad de rotura de la viruta, y también se puede definir como la velocidad de deslizamiento de la viruta respecto a la pieza. Esta velocidad se define a partir del valor de la velocidad de corte, mediante la siguiente fórmula:

	sen (π/2 - γ)
Vs = Vc ·
	sen (γ + π/2 + φ)

donde,

V_s    es la velocidad de deformación, expresada en metros por minuto (m/min)

V_c    es la velocidad de corte, expresada en metros por minuto (m/min)

γ    es al ángulo de desprendimiento

φ    es al ángulo de deslizamiento o cizalladura

•  Velocidad de salida de la viruta (V_v) : Es la velocidad de salida de la viruta respecto a la herramienta. Esta velocidad también se calcula a partir del valor de la velocidad de corte, mediante la siguiente fórmula:

	sen (φ)
Vv = Vc ·
	sen (γ + π/2 + φ)

donde,

V_v    es la velocidad de salida de la viruta, expresada en metros por minuto (m/min)

V_c    es la velocidad de corte, expresada en metros por minuto (m/min)

γ    es al ángulo de desprendimiento

φ    es al ángulo de deslizamiento o cizalladura

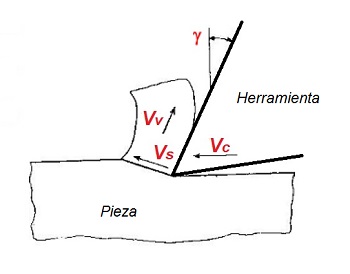
Estas tres velocidades, velocidad de corte (V_c), velocidad de deformación (V_s) y velocidad de salida de la viruta (V_v), se pueden relacionar mediante la siguiente ecuación:

Vs	=	Vv	=	Vc
cos γ		sen φ		cos (φ - γ)

Si en un proceso de mecanizado se tiene una velocidad de corte demasiado baja, la productividad en el corte será muy pequeña y por el contrario, si es demasiado alta, la herramienta se desgastará rápidamente.

La elección de una velocidad de corte adecuada a cada proceso de mecanizado deberá realizarse teniendo en cuenta varios factores entre los que se destacan, el tipo de material de la pieza, el material de la herramienta, la sección de viruta, el refrigerante empleado, etc.

Normalmente en los catálogos de los fabricantes de cada máquina herramienta se indican valores orientativos de las velocidades de corte que se deberán emplear en función del tipo de material a mecanizar.

 

Fuerzas que actúan en el corte ortogonal

Conocer las distintas fuerzas de corten que actúan en un proceso de mecanizado sirve para evaluar las distintas solicitaciones a las que están sometidas tanto la herramienta de corte como la propia pieza, así como para poder determinar el valor de la potencia que es necesaria para realizar el proceso de corte.

La mayor parte de esta potencia se emplea en el proceso de la eliminación del material de la pieza (deformación), de manera que de todas las fuerzas actuantes, la que más interesa conocer es aquella que tiene la misma dirección que la velocidad de corte. A esta componente es a la que habitualmente se denomina como Fuerza de corte (F_c).

Además de la fuerza de corte (F_c) existe otra componente perpendicular a ella denominada fuerza tangencial o normal (N_c), la cual coincidirá con la Fuerza de avance (F_a = N_c).

Estas dos componentes de fuerza (F_c y N_c) dan lugar a una resultante final de fuerzas (F), la cual no actúa exactamente en el filo de la herramienta, sino que su zona de aplicación dependerá del valor del ángulo de desprendimiento (γ). Así, se tiene que cuanto más pequeño sea éste, más alejada estará la resultante de fuerzas (F) del filo de corte de la herramienta.

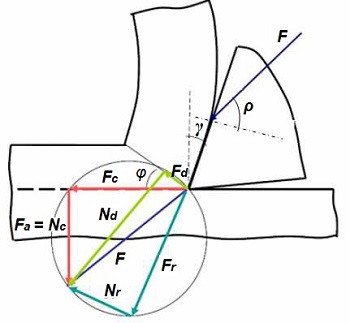
El ángulo (ρ) con el que actúa la fuerza resultante (F) es a priori desconocido. No obstante, esta resultante (F) se puede proyectar según tres sistemas de fuerzas, referidas en diferentes direcciones. De esta manera se tienen:

- La Fuerza de corte, F_c

- La Fuerza de deslizamiento, F_d

- La Fuerza de rozamiento entre la viruta y la herramienta, F_r

Siendo las direcciones de actuación de estas fuerzas las siguientes:

- Dirección del movimiento principal de corte y su normal: F_c  y  N_c = F_a

- Dirección del plano de cizalladura y su normal: F_d  y  N_d

- Dirección de la superficie de desprendimiento de la herramienta y su normal: F_r  y  N_r

La suma vectorial de las distintas componentes de fuerza sería la siguiente:

F→  =  F_c→ + N_c→  =  F_r→ + N_r→  =  F_d→ + N_d→

siendo:

F = Fuerza resultante final del proceso de corte

F_c = Fuerza de corte, que permitirá conocer la potencia necesaria para llevar a cabo el corte de la pieza

F_d = Fuerza de deslizamiento, relacionada con las tensiones cortantes en el plano donde se produce la viruta

F_r = Fuerza de rozamiento entre la viruta y la herramienta

ρ = Angulo de rozamiento

Haciendo uso de las relaciones trigonométricas que se deducen de la anterior figura, se pueden deducir las siguientes expresiones que permiten calcular las distintas fuerzas que intervienen en el corte:

F_c = F · cos (ρ - γ)

N_c = F_a = F · sen (ρ - γ)

F_d = F · cos (φ + ρ - γ)

N_d = F · sen (φ + ρ - γ)

F_r = F · sen ρ

N_r = F · cos ρ

De las dos últimas ecuaciones se puede calcular el coeficiente de fricción (µ_roz) que se produce entre la viruta y la superficie de desprendimiento de la herramienta. Este coeficiente suele ser constante en toda la longitud de contacto.

En un proceso de mecanizado convencional de metales usuales, los coeficientes de fricción medidos suelen tener valores elevados (0.5 < µ_roz < 2) en comparación con los valores medidos en un contacto convencional del mismo material.

A continuación, se muestra la expresión que permite calcular el coeficiente de rozamiento (µ_roz) entre la viruta y la herramienta:

	Fr
µroz  =  tan ρ  =
	Nr

 

Estudio de la viruta generada en el corte

Como se sabe, la viruta es todo aquel fragmento de material residual, que típicamente suele adoptar una forma de lámina curvada o espiral, y que se desprende del material de la pieza durante el proceso de mecanizado.

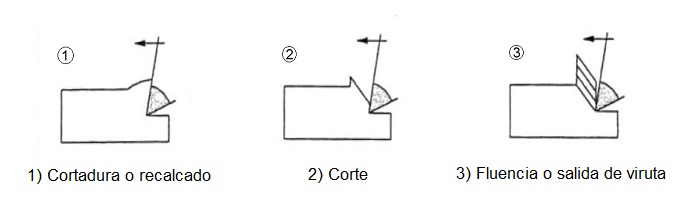
Cabe decir que toda viruta generada se separa del material base de la pieza por la combinación de tres procesos sucesivos:

1) Cortadura o recalcado: el material es desplazado por el filo de la herramienta de corte, que va penetrando en él.

2) Corte: una parte de la viruta se corta debido a que el esfuerzo cortante es mayor que la resistencia al corte del material que forma la viruta.

3) Fluencia o salida de viruta: dependiendo de cómo sea el material y de otros factores que se verán más adelante, se produce el desprendimiento de la viruta que puede ser en forma segmentada, discontinua, o bien formando una viruta toda continua.

Entre los parámetros de corte que definen los procesos de mecanizado, ya vistos en apartados anteriores, también habrá que incluir otro más: la sección de la viruta. La sección de viruta (S) se calcula como el producto del avance (a) por la profundidad en el corte (p):

S = a · p

donde,

S    es la sección de viruta, expresado en milímetros cuadrados (mm²)

a    es el avance, expresado en milímetros (mm.)

p    es la profundidad de corte, expresado en milímetros (mm.)

En general, la sección de la viruta generada dependerá de la potencia de la máquina de corte, la rigidez de la máquina y la fijación de la herramienta.

Multiplicando la sección de viruta por la velocidad de corte se obtiene el arranque de material (Q). Este dato sirve para calcular el volumen de viruta arrancada por unidad de tiempo, dato muy útil en las operaciones de desbaste de piezas.

Q = V_c · S · 1000

donde,

Q    es el volumen de arranque de material, expresado en (mm³/min)

S    es la sección de viruta, expresado en milímetros cuadrados (mm²)

V_c    es la velocidad de corte, expresada en metros por minuto (m/min)

La viruta, como parte de material que se arranca de la pieza, tiene dos superficies: la que ha estado en contacto con la cara de ataque de la herramienta y que posee una apariencia brillante y pulida, debido al continuo rozamiento al desplazarse sobre la superficie de la herramienta; y la otra cara de la viruta que proviene de la superficie de la pieza, siendo su apariencia rugosa y mellada debida al propio proceso de corte.

La forma geométrica que adopte la viruta generada durante el corte depende de la forma de la herramienta y de las condiciones de corte, y es una característica muy relevante que permite deducir si las operaciones de mecanizado se están llevando de una manera óptima.

Una rotura corta de la viruta, con discontinuidad o segmentación de la misma es una solución óptima en el proceso de corte, ya que no afectará a la superficie mecanizada ni a los elementos que la rodean.

A continuación, se incluyen los principales tipos de viruta que pueden darse en las operaciones de mecanizado:

•  Viruta continua: las virutas continuas se forman cuando se mecanizan materiales dúctiles, con pequeños avances y a altas velocidades de corte, o bien, cuando se disponen de ángulos de desprendimiento elevados. Una viruta continua que no se rompa es molesta y se suele evitar.

Con una velocidad de corte convencional, la temperatura de la viruta sin deformar es menor y la que se genera lo hace por cizalladura en la zona primaria de corte. Esta zona de la viruta está muy deformada, y se produce un endurecimiento del material por deformación que dificulta su rotura, lo que dará lugar a una viruta continua.

Aunque por lo general producen un buen acabado superficial en la pieza, las virutas continuas no son siempre deseables, ya que tienden a atorarse alrededor de los portaherramientas, los soportes y la pieza de trabajo, lo que obliga a veces a tener que detener la operación de mecanizado para limpiar los residuos que se generan.

No obstante, este inconveniente se puede solventar empleando un rompevirutas, artilugio que suele venir incorporado a la geometría de filo de la herramienta y cuya función es obligar a la viruta a salir con un radio más pequeño provocando su ruptura por tensión.

•  Viruta segmentada: las virutas segmentadas se presentan semicontinuas, con grandes zonas de baja deformación cortante y pequeñas zonas de alta deformación cortante. Este comportamiento se muestra en el mecanizado de materiales tenaces, en metales con baja conductividad térmica y resistencia, que disminuyen en forma abrupta con la temperatura, más notablemente en el titanio, y utilizando bajas velocidades de corte.

•  Viruta discontinua: son virutas que se presentan discretizadas en segmentos que pueden estar firmemente sujetos unos a otros, o muy sueltos. Se suelen presentar durante el mecanizado de materiales frágiles, duros y quebradizos ya que no tienen la capacidad de soportar la deformación cortante. También se generan cuando se usan velocidades de corte muy bajas. En este caso, la evacuación de este tipo de viruta se realiza fácilmente, dado que se desprende conforme se va produciendo.

La formación de este tipo de viruta ocasiona que la fuerza de corte varíe constantemente durante el corte. Por tanto, si el portaherramientas, los dispositivos de sujeción de la pieza y la máquina herramienta no son suficientemente rígidos pueden producirse vibraciones y traqueteos, lo que puede causar un desgaste prematuro de la herramienta de corte.

Por último merece la pena reseñar un fenómeno relacionado con los procesos de formación de viruta, que es el filo recrecido.

En los procesos de corte por mecanizado, el material de la pieza está sometido a una gran presión y altas temperaturas. En estas condiciones se crea una zona de acumulación de material a continuación del filo de la herramienta de corte. Entonces ocurre que el material deformado se va uniendo al filo de la herramienta cubriendo parte de éste.

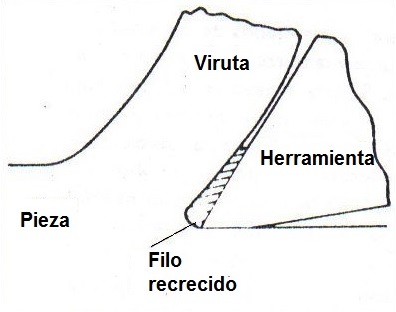
Dependiendo de las condiciones en que se produzca el corte, se puede dar el caso de que la generación de estas capas sea sucesiva a lo largo de todo el proceso y se vayan uniendo y soldando unas sobre otras, dando lugar al llamado filo recrecido.

Este fenómeno aparece normalmente cuando se trabaja con materiales dúctiles y a bajas velocidades, que produce la soldadura o fusión de partículas de viruta con la cuchilla de corte.

En general, este fenómeno hay que evitarlo, ya que provoca un acabado de mala calidad y vibraciones debido a que se generan altas presiones en la zona de contacto viruta-herramienta.

Aumentar la velocidad de corte, lubricar, utilizar materiales de herramienta adecuados, como metales duros o cerámicas, o aumentar el ángulo de desprendimiento son algunas de las soluciones más comunes y efectivas que se pueden tomar para acabar con el fenómeno del filo recrecido.

          Modelos de análisis de los procesos de mecanizado

En los procesos de fabricación mecánica resulta muy importante poder conocer con la mayor exactitud posible el comportamiento de un material al que se está sometiendo a un proceso cualquiera de mecanizado. Por otro lado, en los procesos de mecanizado, el material se encuentra sometido a una serie de cargas dinámicas, y su estudio, que generalmente resultará complejo, puede llevarse a cabo por distintos métodos empíricos, analíticos o numéricos.

PROGRAMA DE COLABORACIÓN

Colabora en el sostenimiento de esta WEB

Los métodos empíricos se basan en la realización de pruebas experimentales reales, de las cuales se pueden extraer cierta información del proceso que se está llevando a cabo, siendo por lo general este tipo de método muy costoso, tanto en tiempo como en dinero. Por su parte, los métodos analíticos utilizan expresiones y fórmulas simplificadas de las diversas fuerzas que actúan sobre el material durante el proceso de mecanizado, y a partir de los criterios de resistencia y rotura simples de los materiales poder deducir otras expresiones sencillas que puedan definir el comportamiento del material durante el proceso de mecanizado.

Sin embargo, son los métodos numéricos los que actualmente están siendo más ampliamente utilizados, y se fundamentan en el uso de programas informáticos de simulación basados en el Método de los Elementos Finitos (MEF).

La idea básica del MEF consiste en obtener un modelo discreto del conjunto de la pieza que se pretende mecanizar. De esta manera, a partir de la pieza que estará sometida a un sistema de cargas y coaccionada por unas ligaduras que mantendrán la pieza fija a la máquina, se dividirá ésta en pequeñas partes (proceso de discretización), denominadas comúnmente elementos, que estarán interconectados entre sí a través de unos puntos, denominados nodos. Las ecuaciones que rigen el comportamiento del material de la pieza también regirán el comportamiento del elemento. De esta manera se pasa de tener un sólido continuo con infinitos grados de libertad, a un sólido discretizado con un número determinado de grados de libertad.

Por tanto, empleando el MEF se ha procedido a discretizar el problema inicial tanto en el espacio como en el tiempo, para posteriormente simular el proceso de mecanizado utilizando potentes ordenadores. La capacidad de tener un resultado fiable con este método numérico depende en gran medida de disponer de modelos fiables que definan el comportamiento de los materiales involucrados. Un modelo completo requiere determinar la ecuación constitutiva que relaciona las tensiones y deformaciones en función de la velocidad de deformación, de la temperatura y finalmente el criterio de rotura del material.

Existen en el mercado distintos software que emplean el método numérico de los Elementos Finitos como el denominado ABAQUS. Este software, como se ha dicho antes, modela el sólido inicial que se pretende mecanizar, dividiendo su forma continua original en un número finito de partes o elementos. A su vez, estos elementos poseen en su contorno los denominados nodos que unen cada elemento con sus adyacentes. Este proceso es lo que se conoce como el mallado de la pieza, y con ello, se consigue reducir el problema inicial a un numero finito de grados de libertad.

Una vez generado el mallado inicial de la pieza, sobre ésta se imponen las diferentes condiciones de contorno derivados de las condiciones de sujeción de la pieza a la máquina de mecanizado y se le asignan las propiedades mecánicas del material. Este programa permite incluso poder redefinir el mallado inicial a una malla más fina en aquellas zonas localizadas de interés, como puedan ser zonas cercanas a agujeros, esquinas entrantes, etc., con el fin de obtener resultados mucho más precisos en dichas zonas.

Mientras dura el proceso de cálculo de simulación, el Método de los Elementos Finitos va obteniendo los valores de los desplazamientos que sufre cada nodo bajo la aplicación de determinas fuerzas. Con los valores de estos desplazamientos y resolviendo las ecuaciones de rigidez que relacionan fuerzas y desplazamientos se consiguen conocer las deformaciones de cada uno de los elementos, y con éstas y aplicando la ecuación constitutiva propia del material, se podrán obtener como solución las tensiones a las que se ve sometido el material del sólido que se está mecanizando.

En definitiva, mediante la aplicación de los métodos numéricos, se pueden obtener una gran cantidad de información de todo proceso de mecanizado (históricos de tensiones, deformaciones, temperaturas, mapas de velocidades) y son métodos mucho menos costosos que realizar estudios empíricos con piezas reales. Por todo ello, y teniendo en cuenta el continuo avance en la capacidad y rapidez de cálculo de los ordenadores, los métodos de simulación numérica se están convirtiendo en una herramienta casi imprescindible en cualquier estudio que se desee realizar del comportamiento de cualquier elemento estructural sometido a un estado de cargas.